A Journey from Resonance to Impedance Matching

Chp. 4: Series to Parallel Conversion using Quality Factor

The Underrated Magic Trick

A series impedance can be transformed to equivalent parallel impedance and vice versa. This is the most underrated trick yet it is fundamental to matching network design. Math behind series to parallel conversion is simple. You want to know when a series impedance is equal to parallel impedance, so you equate them.

R_s + jX_s = R_p \,||\, jX_p $$ $$ R_s + jX_s = \frac{jR_pX_p}{R_p+jX_p}$$ $$ R_s + jX_s = \frac{R_pX_p^2}{R_p^2+X_p^2}+j\frac{R_p^2X_p}{R_p^2+X_p^2}$$ $$ R_s + jX_s = \frac{R_p}{\frac{R_p^2}{X_p^2}+1} +j\frac{X_p}{1+\frac{X_p^2}{R_p^2}}$$ $$ R_s + jX_s = \frac{R_p}{Q^2+1}+j\frac{X_p}{1+\frac{1}{Q^2}}$$ $${\large \textcolor{#40CE7F}{\implies R_p = R_s\,(1+Q^2) \;\;\;\text{&}\;\;\; X_p = X_s \left(1+\frac{1}{Q^2}\right)}}

This says a series R_s is boosted by factor (1+Q²) when it is converted to a parallel resistance, and a series reactance X_s is boosted by factor (\(1+\frac{1}{Q^2}\)) when it is converted to a parallel reactance. For Q>>1 (or practically Q>4) this translates to

{\large \textcolor{#40CE7F}{\implies R_p = Q^2R_s\;\;\;\text{&}\;\;\; X_p = X_s \;\;\; (1)}}

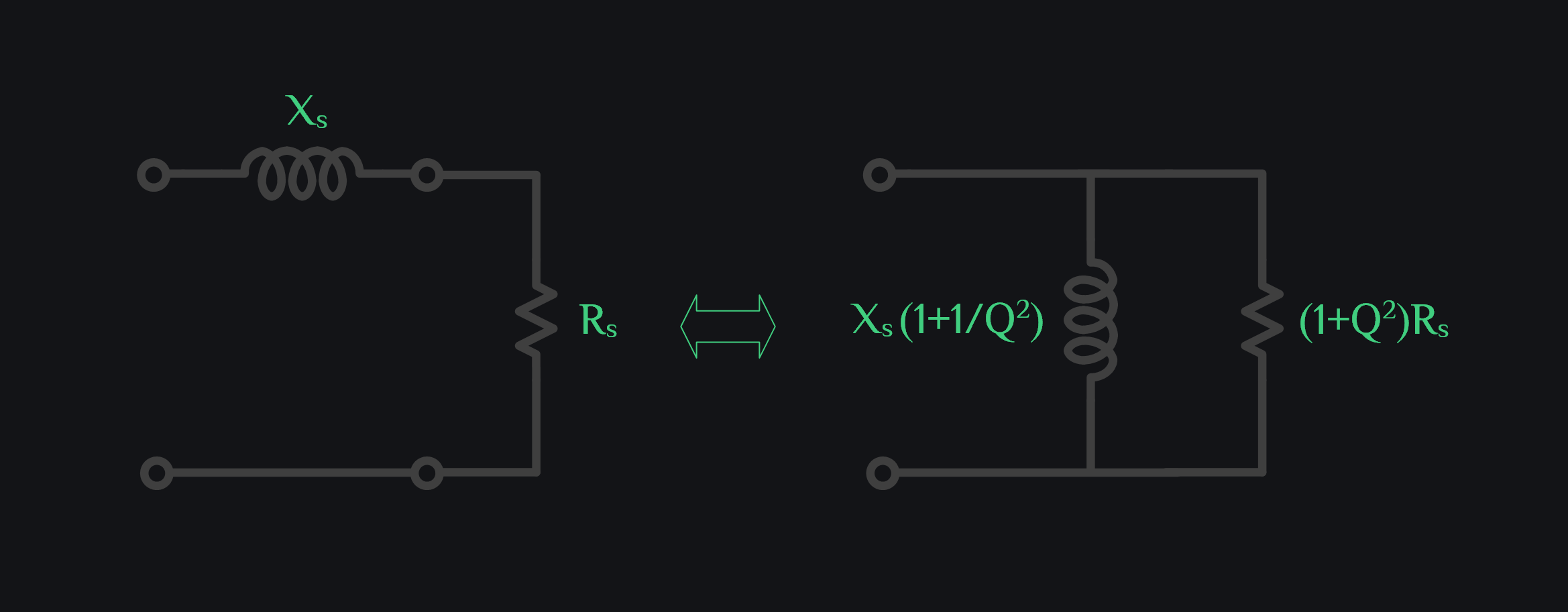
This means a resistor got boosted but reactance stayed same which is strange. Let’s explore the physical explanation of why is it so.

Intuition behind Series to Parallel Conversion

Excite a series RL circuit with voltage V_S as shown in image below.

V_S = V_R + j QV_R $$ $$ V_S = V_R(1+jQ)$$ $$|V_S| = |V_R|\sqrt{1+Q^2} \;\;\;\; (2) $$ $$\implies |V_R| = \frac{|V_S|}{\sqrt{1+Q^2}}

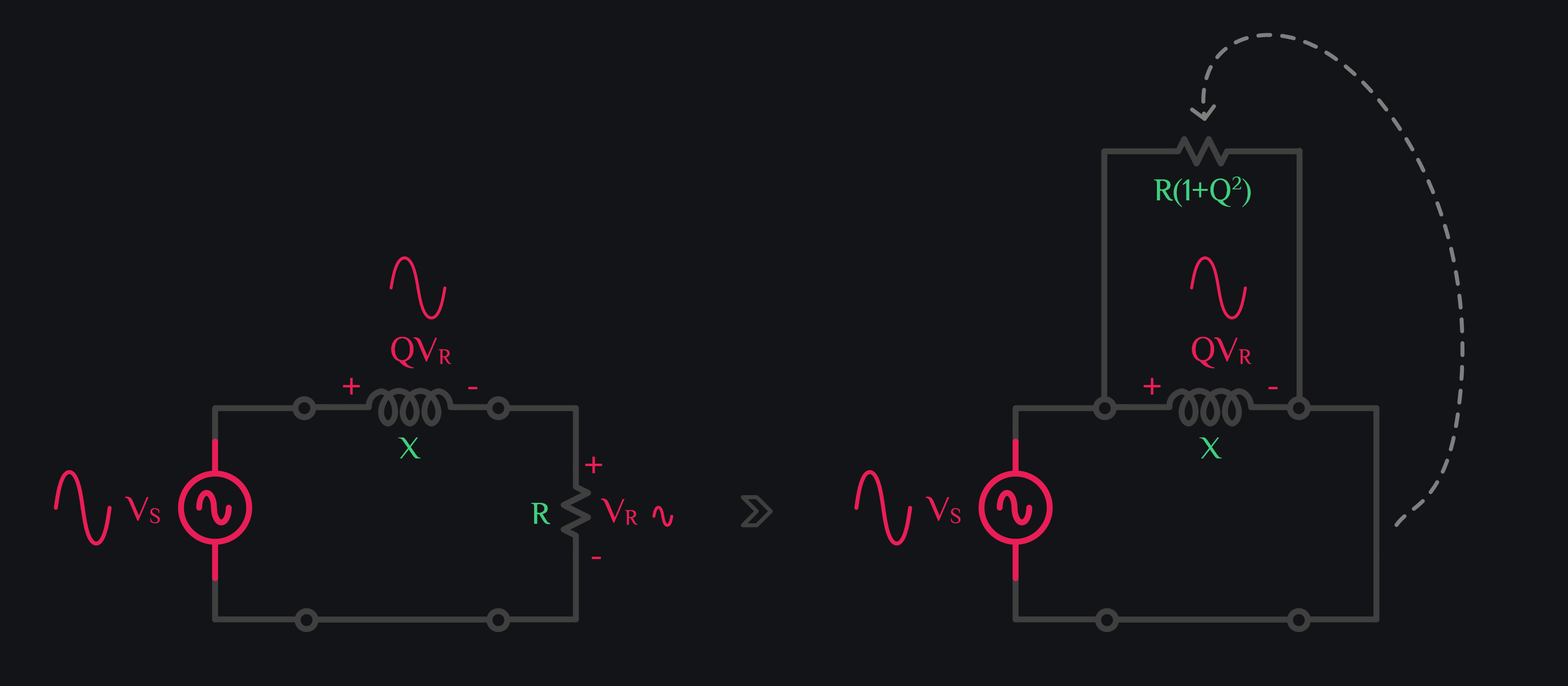
Power dissipated by resistor can be given as:

P = \frac{1}{2}\,\frac{V_R^2}{R} $$ $$ P = \frac{1}{2}\,\frac{V_S^2}{R\,(1+Q^2)} \implies \text{as if } V_S \text{ is delvering power to a resistor }R(1+Q^2)

Now this is interesting. Think about it. It says if you were to apply the whole voltage V_s across the resistor, the resistor would need to go up by 1+Q² to keep the power same. If you don’t increase the resistor, the power drop across resistor would be huge because it sees the whole V_S now instead of small V_R as it saw in series case. This is why a series resistor gets a boosting factor of 1+Q² in its parallel equivalent counterpart.

Physically it means voltage across R increased by factor Q. Remember in a series RL circuit, if a resistor has V_R voltage, the inductor would have QV_R voltage. Now when you move this resistor in parallel to inductor, resistor also taps a bigger voltage QV_R. So if voltage goes up by Q, power goes by up Q², therefore R also has to go up by Q² to keep overall power same. Or you can say if voltage goes up by Q, current has to go down by Q to keep the power same (just like a transformer where if voltage goes up by turn ratio N, current goes down by N). So ratio \(\frac{QV}{\frac{I}{Q}}\) gives you \(Q^2\frac{V}{I}\) i.e., Q² times higher impedance. Ok wait, you just said that it gets boosted by 1+Q², and now you say Q². Where did 1 go? To give you intuition behind boosting (i.e., resistor tapping a bigger voltage now), we said this bigger voltage is QV_R but it is actually V_S and that is almost equal to QV_R for Q>>1 as revealed by Eq. (2). So, the factor 1 is there if you want to be very precise, but it wouldn’t be unfair to say Q is usually much greater than one, and to keep things simple (and memorable), we can just say impedance is boosted by Q².

Why won’t inductor boost by factor Q² as well?

Now that we argued that it makes sense for a series resistor to get boosted by factor Q² when we place the resistor in parallel, you may ask why didn’t it happen to inductor because Eq. (1) tells us reactance stays almost same.

Let’s go back to series RL circuit. Inductor already had big voltage across it QV_R. Going from series to parallel did not get it much bigger of voltage boost. It was QV_R in series, and it is V_S now in parallel. And as stated before, QV_R is almost equal to V_S for Q>>1. Therefore inductor value only has to go up a little to keep reactive power same. If inductor also gets a boost of Q², it will draw huge reactive power, then we can’t say this parallel impedance is equal to series impedance because series inductor would have been drawing relatively small reactive power. And when Q is small, then yes boost in inductance is also visible. For Q>>1, you just don’t see much boost, so it is fair to say series and parallel reactance stays same.

Let’s run quick math to see this through. Reactive power across inductor in series RL circuit can be given as:

Q = \frac{1}{2}\,\frac{(QV_R)^2}{X} $$ $$ Q = \frac{1}{2}\,\frac{Q^2V_S^2}{X\,(1+Q^2)} \;\;\; \text{because}\; V_R = \frac{V_S}{\sqrt{1+Q^2}}$$ $$ Q = \frac{1}{2}\,\frac{V_S^2}{X\,(1+\frac{1}{Q^2})}\implies \text{as if } V_S \text{ is delvering reactive power to a reactance }X\left(1+\frac{1}{Q^2}\right)

Is Series to Parallel Conversion Narrowband?

Note that a common misconception that exists is that this series to parallel impedance transformation is narrowband. The transformation itself is not narrow band, it is Q. Quality factor changes over frequency, and you need to update R and X values based on frequency. If you can do that, it is as wideband as you want. But you won’t be able to do that. Your typical case of use would be: you figured out what is parallel equivalent of your series circuit at one frequency, you went ahead and replaced that series circuit with parallel one. So that’s that. At that frequency, your series and parallel circuit would behave exactly same, at frequencies nearby their response would still be similar because Q wouldn’t have changed much, but once you start looking at far off frequencies, all bets are off because Q would have changed a lot.

RFInsights

Published: 18 Feb 2023
Last Edit: 18 Feb 2023

A Journey from Resonance to Impedance Matching

Intuition behind Series to Parallel Conversion

Why won’t inductor boost by factor Q2 as well?

Is Series to Parallel Conversion Narrowband?

Browse by Tags

Why won’t inductor boost by factor Q² as well?