Passive Mixers

Chp. 1: Input Impedance of Switched Resistor

In this post, we analyze the input impedance of a resistor that is periodically switched on and off, and compare it with the impedance of a continuous (unswitched) resistor. We then explore how this switching behavior enables impedance transformation, a key principle in passive mixers and switched-capacitor circuits.

1.1 When a Resistor is Switched ON & OFF

1.1.1 When Input is DC

Let’s start simple. Assume you have a 1k\(\Omega\) resistor connected to 1V DC. It would draw 1mA. What if we put a switch in-between? When switch turns ON, resistor draws current and when switch turns OFF, no current flows. Alright, now let’s say switch turns ON 50% of the time and remains OFF 50% of the time (in other words duty cycle is 50%), intuitively you would expect that since source is providing 1mA half the time and zero the other half, on average 0.5mA is drawn from the source i.e., DC current is 0.5mA. Hmm as if resistor value is doubled (meaning if there was no switch, a 2k\(\Omega\) would draw 0.5mA but now with switch even 1k\(\Omega\) is drawing 0.5mA). This means switching things ON and OFF can transform impedance. So, matching networks (Ls & Cs) are not the only way to match impedance.

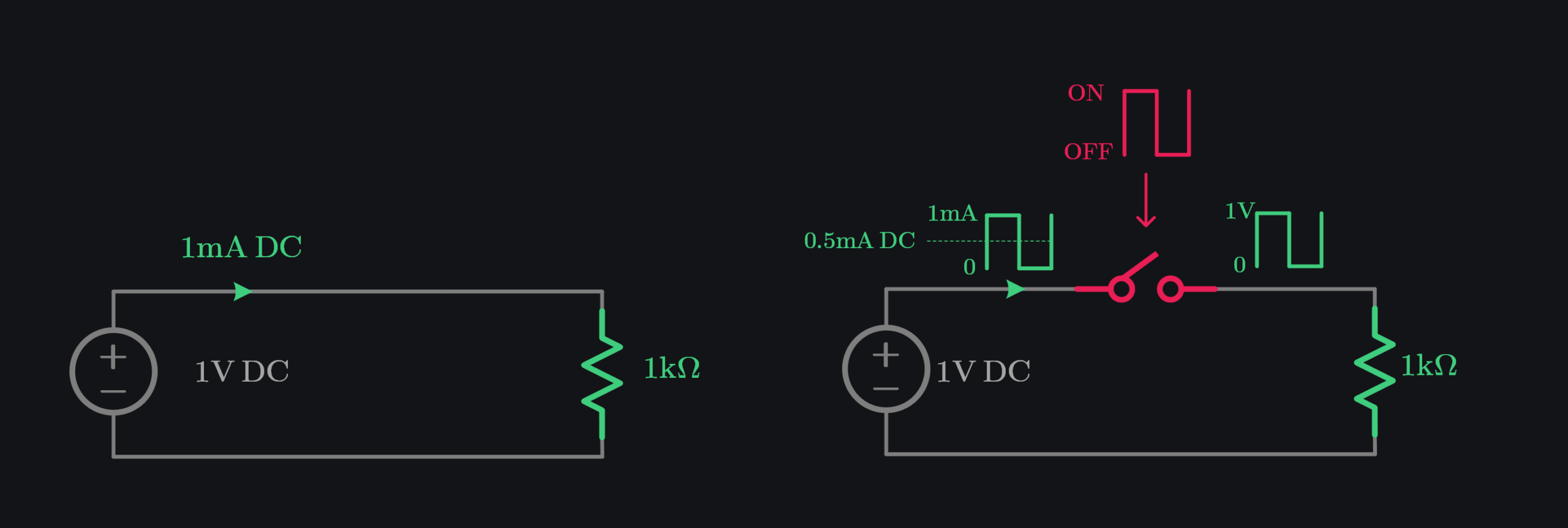
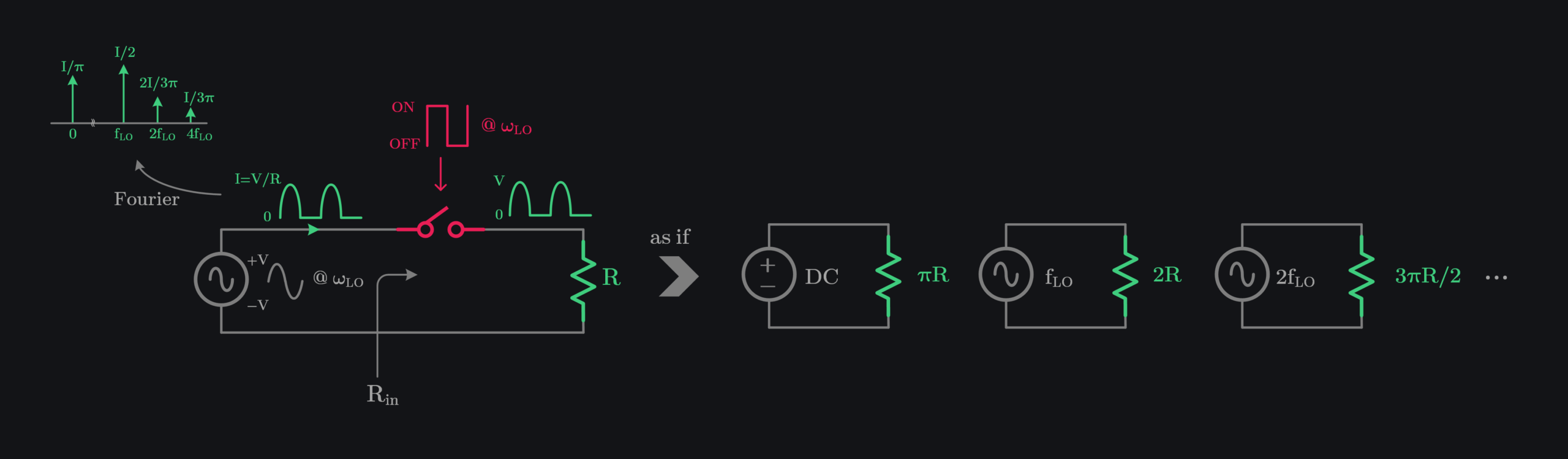
Let’s develop this mathematically. Say, switch is turned ON and OFF by frequency \(\omega_{LO}\), load is a resistor R, and source is DC with amplitude V. Current drawn from source would look like a square wave toggling between 0 and amplitude \(\frac{V}{R}\), and can be written as:

\large I= \frac{V}{R}\left[\frac{1}{2} + \frac{2}{\pi}cos(\omega_{LO}t)- \frac{1}{3}\frac{2}{\pi}cos(3\omega_{LO}t)+ \frac{1}{5}\frac{2}{\pi}cos(5\omega_{LO}t)+\,...\right]\;\;\; (1)

Now wait, there is something here. We see at DC current drawn is \(\frac{1}{2R}\) which matches with our intuition, but we are also drawing current at harmonics of \(\omega_{LO}\). This also makes sense since current drawn looks like a square wave and we know square wave is rich at odd harmonics. But your source in only DC, how come it can provide current at LO frequency? Simple way to think about is to imagine in time domain. In time domain, you are simply taking constant current \(\frac{V}{R}\) from source when switch is ON and 0 when OFF, that’s all source is providing.

What is of significance here is that the fact that some current being drawn at LO frequency and its harmonics means you are seeing some impedances at these frequencies. This is as if your resistor \(R\) is transformed to \(\frac{\pi}{2}R\) at \(\omega_{LO}\), to \(\frac{3\pi}{2}R\) at \(3\omega_{LO}\), and so on as per (1). Thus, we can write input impedance of a switched resistor as:

{\large \begin{align*} R_{in} &= 2R && \text{(at DC)} \\ &+ \frac{\pi}{2}R && \text{(at } \omega_{LO} \text{)} \\ &- \frac{3\pi}{2} R && \text{(at } 3\omega_{LO} \text{)} \\ &+ \dots && \end{align*} }

What does negative sign mean? We will answer shortly.

1.1.2 When Input is of Same Freq as CLK

Let’s break it down with another example to fully grasp the concept. Say now input is a sinusoid with frequency \(\omega_{LO}\) and amplitude \(V\), and our switch is also turning ON and OFF at frequency \(\omega_{LO}\). When switch is ON, sinusoid go through and drives resistor \(R\). When switch is OFF, no current flows. The current drawn from source will look like a switched sinusoid as shown in image below. We can model this by saying this is as if a square wave toggling between 0 and 1 multiplied with our sinusoid.

\large \begin{aligned} I &= \text{Signal} \cdot \text{Square Wave} \\ \\ I &= \frac{V}{R} \cos(\omega_{LO}t) \cdot \left[\frac{1}{2} + \frac{2}{\pi} \cos(\omega_{LO}t) - \frac{2}{3\pi} \cos(3\omega_{LO}t) + \dots \right] \\ \\ I &= \frac{V}{R} \left[ \frac{1}{2} \cos(\omega_{LO}t) + \frac{2}{\pi} \cos(\omega_{LO}t) \cos(\omega_{LO}t) - \frac{2}{3\pi} \cos(\omega_{LO}t) \cos(3\omega_{LO}t) + \dots \right] \\ \\ I &= \frac{V}{R} \left[ \frac{1}{2} \cos(\omega_{LO}t) + \frac{1}{\pi} \left(1 + \cos(2\omega_{LO}t)\right) - \frac{1}{3\pi} \left( \cos(2\omega_{LO}t) + \cos(4\omega_{LO}t) \right) + \dots \right] \\ \\ I &= \frac{V}{R} \left[ \frac{1}{\pi} + \frac{1}{2} \cos(\omega_{LO}t) + \left(\frac{1}{\pi} - \frac{1}{3\pi}\right) \cos(2\omega_{LO}t) - \frac{1}{3\pi} \cos(4\omega_{LO}t) + \dots \right] \\ \\ I &= \frac{V}{R} \left[ \frac{1}{\pi} + \frac{1}{2} \cos(\omega_{LO}t) + \frac{2}{3\pi} \cos(2\omega_{LO}t) - \frac{1}{3\pi} \cos(4\omega_{LO}t) + \dots \right] \end{aligned}

Thus, input impedance can be written as:

{\large \begin{align*} R_{in} &= \pi R && \text{(at DC)} \\ &+ 2R && \text{(at } \omega_{LO} \text{)} \\ &+ \frac{3\pi}{2}R && \text{(at } 2\omega_{LO} \text{)} \\ &+ \dots && \end{align*} }

1.1.3 General Formula for Switched Resistor Input Impedance

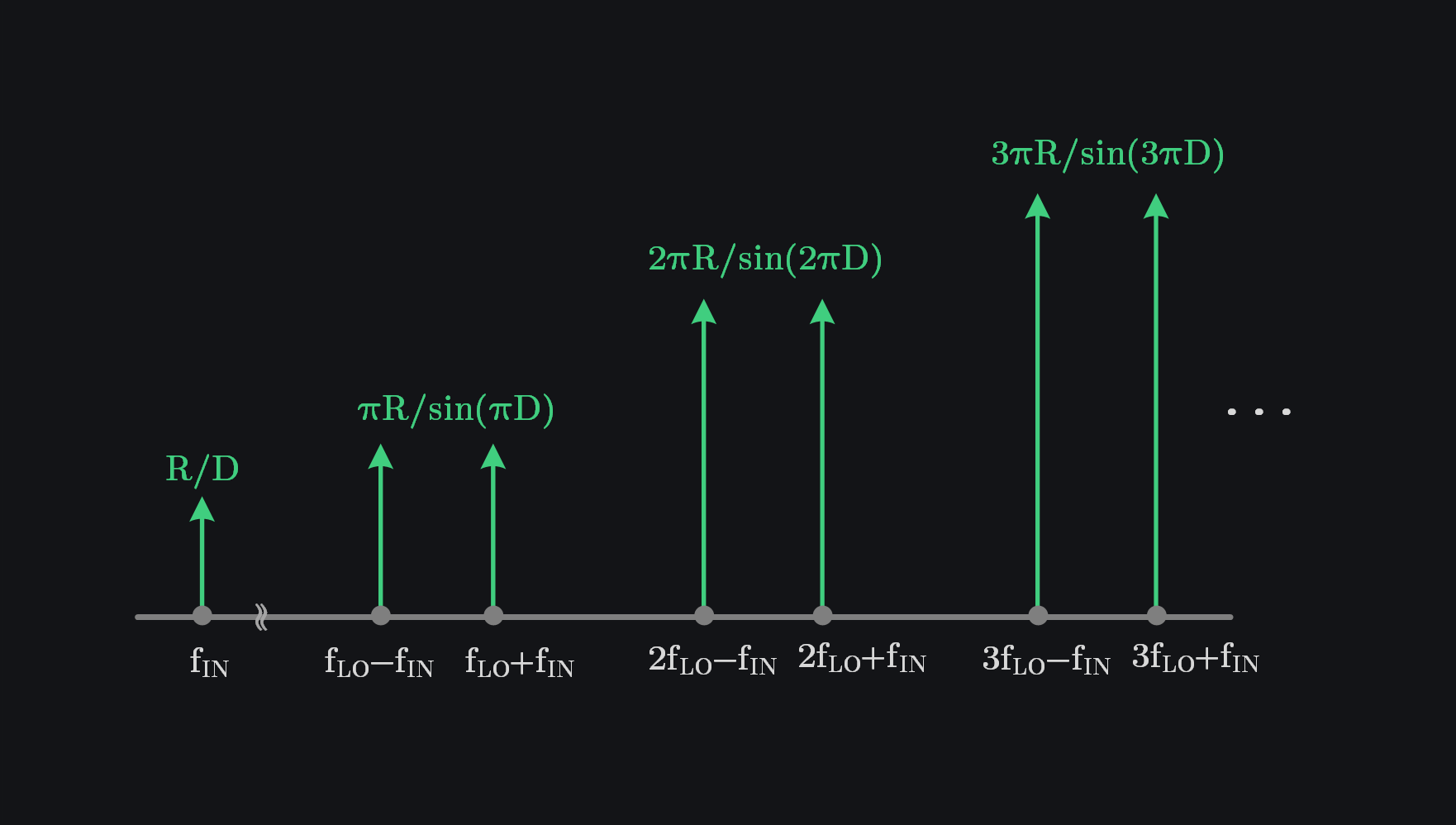
In general, for an input signal of frequency \(\omega_{IN}\) with 50% duty cycle driving a resistor R through a switch toggling at frequency \(\omega_{LO}\) and , we can write input resistance to be:

{\large \begin{align*} R_{in} &= 2R && \text{(at } \omega_{IN} \text{)} \\ &+ \pi R && \text{(at } \omega_{LO} - \omega_{IN} \text{)} \\ &+ \pi R && \text{(at } \omega_{LO} + \omega_{IN} \text{)} \\ &- 3\pi R && \text{(at } 3\omega_{LO} - \omega_{IN} \text{)} \\ &- 3\pi R && \text{(at } 3\omega_{LO} + \omega_{IN} \text{)} \\ &+ \dots && \end{align*} }

where,

R transforms to 2R at \(\omega_{IN}\) because of 50% duty cycle. You are only drawing current half the time, and this makes your load look like 2x.
Factor of \(\pi\) appears with R at \(\omega_{LO}-\omega_{IN}\) and \(\omega_{LO}+\omega_{IN}\) because fundamental coefficient of square wave is \(\frac{2}{\pi}\) which splits into sum and difference product and thus gets halved to \(\frac{1}{\pi}\). Meaning current drawn is scaled by \(\frac{1}{\pi}\) i.e., as if resistance is scaled by \(\pi\).
Factor of \(3\pi\) appears with R at \(3\omega_{LO}-\omega_{IN}\) and \(3\omega_{LO}+\omega_{IN}\) because third harmonic coefficient of square wave is \(\frac{2}{3\pi}\) which splits into sum and difference product and thus gets halved to \(\frac{1}{3\pi}\). Meaning current drawn is scaled by \(\frac{1}{3\pi}\) i.e., as if resistance is scaled by \(3\pi\). Note the negative sign. Is it a negative resistor? Yes. Can it be used? Maybe if you get creative. Let’s say you excite your circuit with \(3\omega_{LO}-\omega_{IN}\) (in addition to existing \(\omega_{IN}\)), it will generate its own “2R” component and that will add to -ive component generated by \(\omega_{IN}\) making the overall impedance positive again. (Note by addition we mean parallel combination since current delivered by each source is in parallel i.e., \(3\omega_{LO}-\omega_{IN}\) will deliver current in addition to existing current established by \(\omega_{IN}\))

1.1.4 Intuition Behind Switched Resistor Input Impedance

We saw that you can transform R to 2R at \(\omega_{IN}\) if you add a switch in-between and toggle it with 50% duty cycle. What if changed duty cycle to 25%? We would see 4R at \(\omega_{IN}\). This means we can transform to any higher impedance; all we need is to choose duty cycle. The reason as explained before is same, if you reduce the duty cycle, you are not drawing the current from your source all the time, this is reflected as less current drawn compared to a continuously-drawn non-switched circuit, and this less current drawn means as if load is bigger.

In general, co-efficient of square wave toggling between 0 and 1 can be given as:

\large C_n = \frac{2}{n\pi} \sin(n\pi D)

where,

D is duty cycle (e.g., 0.5 for 50%)
n is harmonic number for n\(\ge\)1

Image below shows how your impedance will look like as a function of duty cycle.

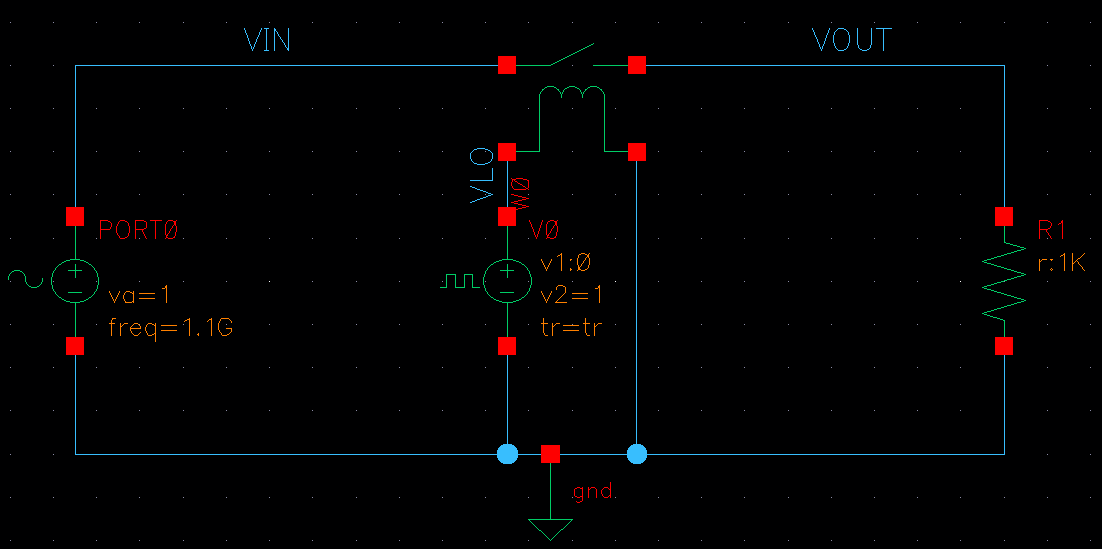
1.1.5 Simulation Verification of Switched Resistor Input Impedance

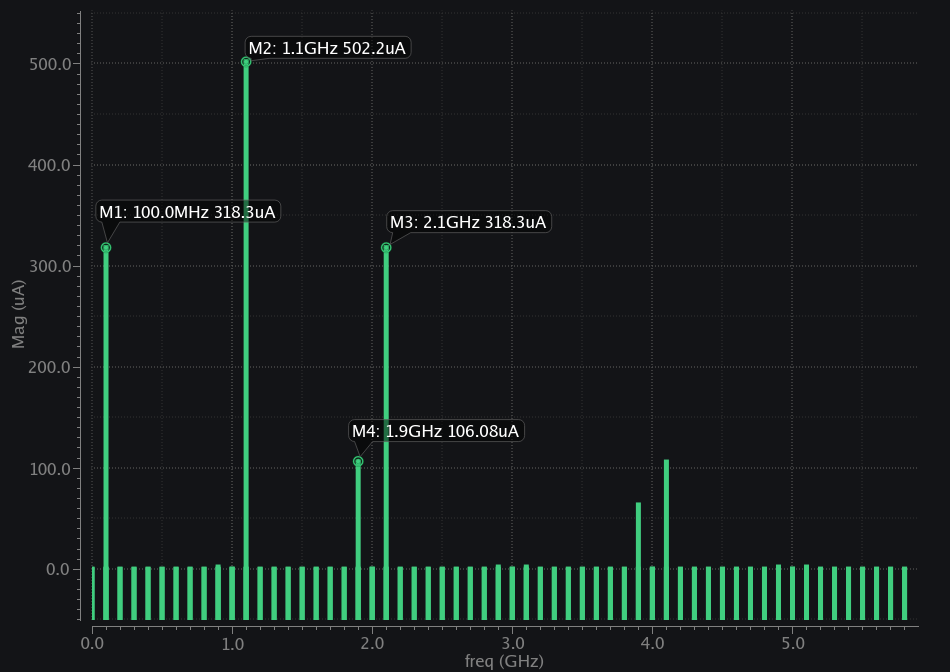
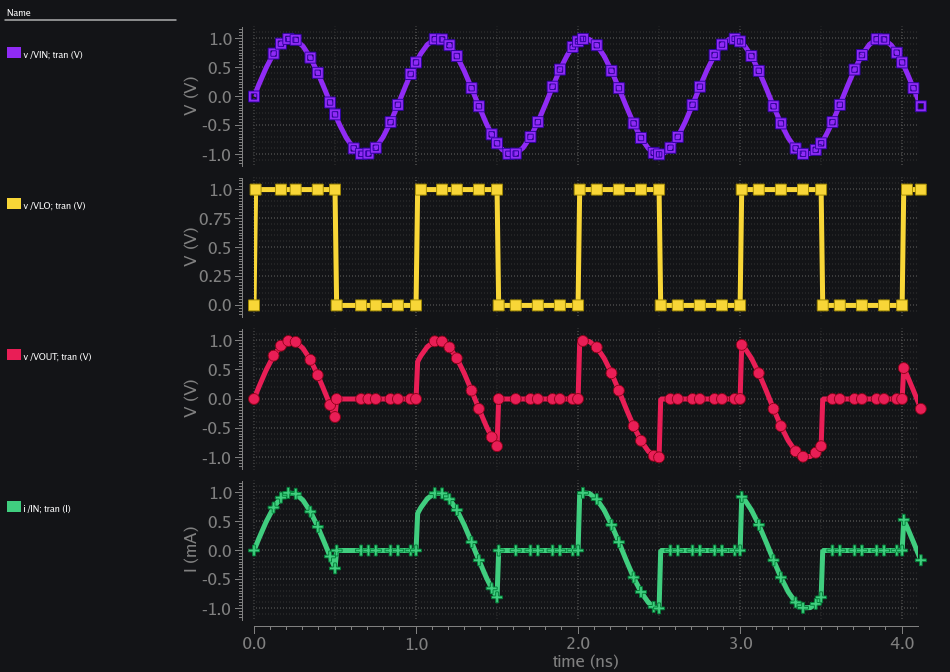
Images below show simulation verification of theory. We used 1k\(\Omega\) resistor, an ideal switch toggled at 1GHz CLK and excite the input with 1.1GHz sinusoid signal . Transient sim plots are shown. Purple being input, yellow CLK, red output voltage, and green input current. We also show input current spectrum. At input frequency of 1.1GHz, we see ~500uA current which means 2k\(\Omega\) resistance which matches with our expectation of \(R_{in}=2R\). We see at 100MHz i.e., \(\omega_{LO}-\omega_{IN}\) & at 2.1GHz i.e., \(\omega_{LO}+\omega_{IN}\) about 318uA current drawn which also matches with our expectation i.e. \(R_{in}=\pi R\) at these frequencies. Similarly, current at 1.9GHz i.e., \(3\omega_{LO}-\omega_{IN}\) is ~106uA which also matches with our expectation i.e. \(R_{in}=3\pi R\)

1.1.6 What if You Switched with Multi-Phase CLK

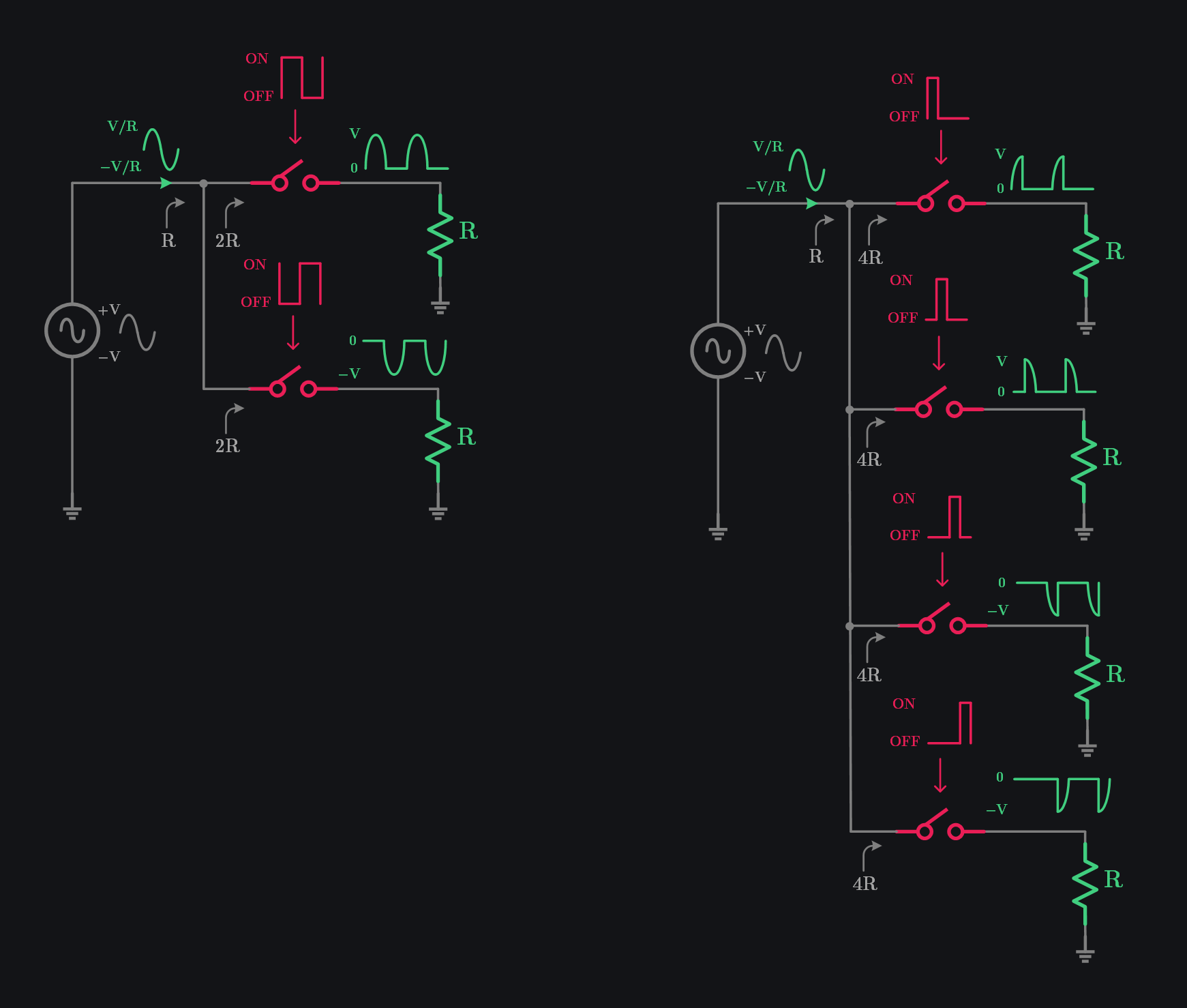
Say, now you use 0 and 180 deg CLK with 50% duty cycle and have schematic like in left figure. Or say, you have four phase CLK with 25% duty cycle and have a schematic like in right figure. What do you think the input current or impedance will look like? Input impedance will be just R, there is no transformation. From input side, current will be always drawn as if it is a continuous system (assuming ideal CLK and thus ignoring transitions). This is because when one switch turns OFF, other will turn ON, and input will continue to see load R all the time. In other words, we can say all those resistors are seen in parallel even though they are never ON at same time!

1.2 When a Resistor is Switched ON & OFF with Current Source

So far, we’ve assumed a voltage source as the input. But what happens if we use a current source instead? After all, input impedance is a property of the circuit. It shouldn’t matter whether we excite the circuit with a voltage source or a current source, right? Right?

Well, now’s the time to read the fine print in textbooks.

This assumption does not hold for time-varying circuits. And switching, even simple on/off switching, introduces time variance. When the switch is ON, the circuit behaves one way. When it’s OFF, it behaves differently. You might think, “But I’m turning the switch on and off in a periodic and predictable way, like an LO continually turning ON and OFF mixer switches. So, does it still count as time-variant?” Yes. If the circuit’s output depends on absolute time, it is time-variant.

And in time-variant systems, the input impedance can change depending on whether you excite the circuit with a voltage source or a current source.

1.2.1 When Input is DC

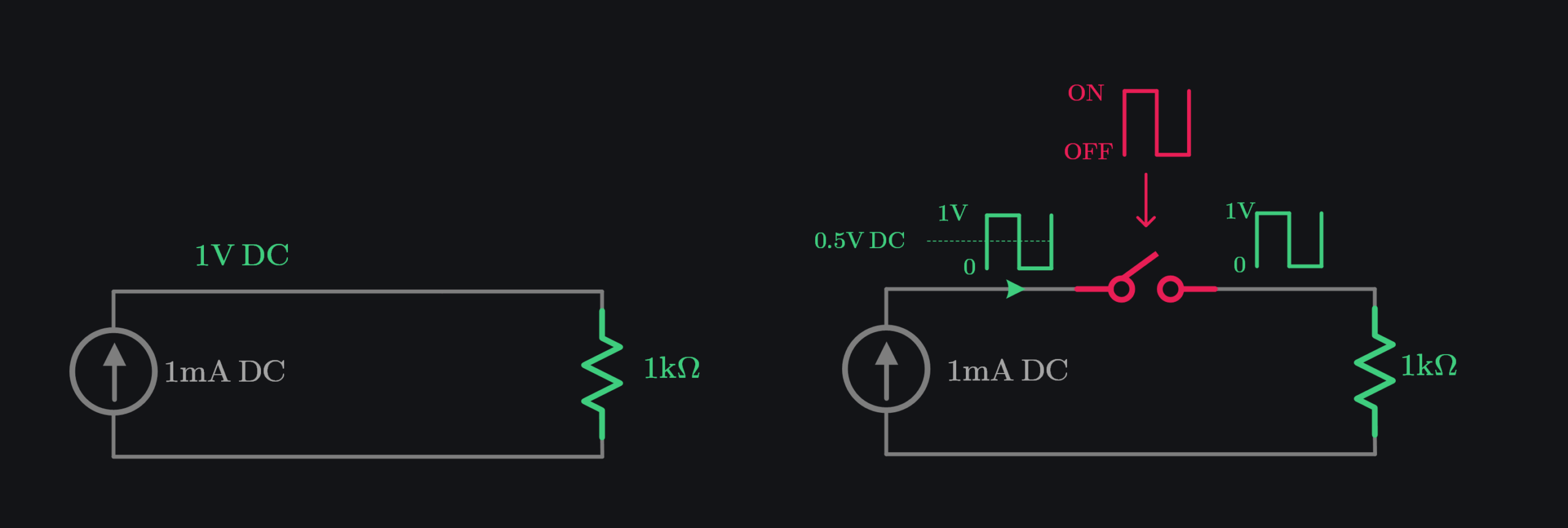
Let’s repeat the same experiment as we did in 1.1.1 but now with current source. It turns out that scalars are flipped. Impedance which was \(2R\) in case of voltage source will look like \(\frac{R}{2} \) for current source. This makes sense because last time we said “Hey, this is as if half the current is drawn so impedance is doubled”, and now we can say, “Hey, this is as if half the voltage is developed so impedance is halved”

Note that when switch is OFF, current still needs a way to flow because it is a current source, we assume it flows into its own output impedance (not shown in image).

1.2.2 General Formula